复利原则
复利是终身成长最为关键的一项原则,然而,其思想与原理却相当简洁。
我们首先看一下它原始的定义:
复利是指在计算利息时,将前一期的利息加入本金,然后再计算下一期利息的一种计息方式。简单来说,就是利滚利”。
例如,你把一笔资金存入银行,银行除了会根据本金支付你利息外,还会把利息也计入下一次计算利息的本金范围,这样随着时间的推移,你的收益会越来越多。
用数学方法来表述复利原则,会更加简洁明了,其数学计算公式如下:

- F是终值,也就是最终的本利和
- P是初始本金
- i是增长利率,例如5%
- n是期数,例如存款的年数
例如,你存入本金1000元,年利率是5%(i=0.05),存期3年(n = 3),那么根据公式计算可得:
F = 1000×(1 + 0.05)^3 = 1000×1.157625≈1157.63元,这里的利息部分为1157.63 - 1000 = 157.63元。
如果是单利计算(只以初始本金计算利息),利息则为1000×0.05×3 = 150元。由此可见,复利比单利能获得更多的收益。
从复利的定义中,我们就能提取出来复利原则的两个核心要素:
- 时间的价值
复利强调时间的重要性。在复利的作用下,即使是很小的利率,经过较长时间的积累,也能产生巨大的增长。
而且时间越长,增加的速度越快,增长曲线呈指数级上升。
- 持续稳定的增长
复利需要有一个持续稳定的增长率才能发挥其最大的威力。持续稳定的增长是复利发挥最大效力的关键。
长期做一件事情,不是机械的重复,而是保持一个持续稳定的增长率。这个增长率可以很小,但在时间的加持下,就可以产生神奇的效果。
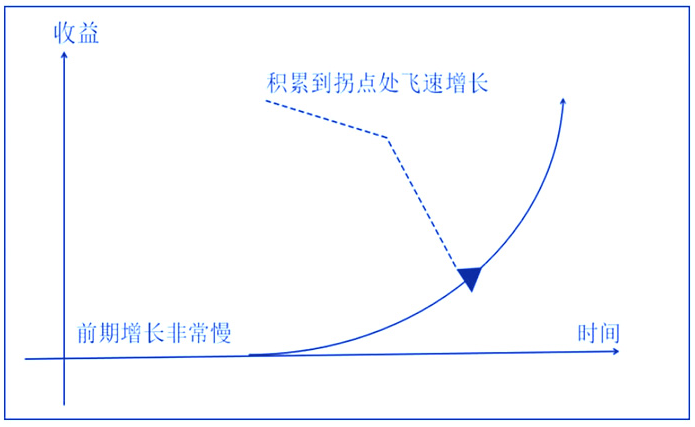
上图曲线呈现出一种典型的复利增长模式:
- 前期增长缓慢:在曲线的起始阶段,增长非常缓慢。这反映了复利在初期由于本金较少,收益增长不明显的特点。例如,在投资初期,即使有一定的回报率,但由于本金不多,收益的绝对值增长较小。
- 积累到拐点处飞速增长:随着时间的推移,曲线在某一点(拐点)之后开始呈现出快速上升的趋势。这是复利的核心特点之一,即经过一段时间的积累,收益会在某一时刻开始迅速增长。这就像在投资中,随着本金和利息的不断累积,后期的收益增长会越来越快。
